백준_16916_부분 문자열

https://www.acmicpc.net/problem/16916

16916번: 부분 문자열

문제

풀이(삽질)

• s와 p가 주어진다. 
• p 글자의 갯수(길이)를 추출하고 p글자의 첫 글자를 s에서 만나면 p글자의 길이만큼 뽑아내서 서로 같은지 비교한다.
  • 비교 시 같으면 바로 break
  • 비교 시 다르면 다시 다음글자 부터 탐색
  • 만약 p의 길이 만큼 뺄수 없다면 try, catch로 0출력 break
• 시간초과!!!
  • for문 한번에 처리해서 O(n)이라고 생각했지만, substring도 n에 가까움...따라서 O(n^2)임.
  • 10만이므로 제곱이면 100만이다. = 시간초과

실수코드

package Simul;

import java.io.BufferedReader;
import java.io.InputStreamReader;

/*
baekjoon
aek
 */

public class 백준_16916_부분문자열 {

    static private String s;
    static private String p;


    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));


        s = br.readLine();
        p = br.readLine();

        //p의 길이 구하기
        int sizeOfp = p.length();
        //p의 첫글자 구하기
        char tempChar = p.charAt(0);
        String tempStr = "";
        //해당 글자 찾기
        int targetNum = 0 ;
        boolean flag = false;
        for(int i = 0 ; i < s.length() ; i++){
            if(s.charAt(i)==tempChar){
                targetNum = i;
                try{
                    tempStr = s.substring(targetNum,targetNum+sizeOfp);
                }catch (Exception e){
                    flag=true;
                    System.out.println(0);
                    break;
                }
                if(tempStr.equals(p)){
                    flag = true;
                    System.out.println(1);
                    break;
                }
            }
        }
        if (!flag)
            System.out.println(0);


    }
}

---

해당 문제는 KMP 알고리즘을 알아야한다.

KMP 알고리즘(참고)

KMP 알고리즘은 반복되는 연산을 줄여나가 매칭 문자열을 빠르게 점프하는 기법으로 효율적으로 문자열 매칭을 이루어나간다.

• KMP 알고리즘을 동작시키기 위해서는 접두사도 되고 접미사도 되는 문자열의 최대 길이를 저장해주는 table을 미리 정의해줘야한다.
• table[]은 patten이 어디까지 일치했는지가 주어질 때 다음 시작 위치를 어디로 해야할지를 말해주기 때문에, 이를 흔히 부분 일치 테이블이라고 부른다.

예를 들어, abacaaba가 있을 때 table[]을 만들어보면 

i	patten(0...i)	접두사이면서 접미사인 최대 문자열	table[i]
0	a	(없음)	0
1	ab	(없음)	0
2	aba	a	1
3	abac	(없음)	0
4	abaca	a	1
5	abacaa	a	1
6	abacaab	ab	2
7	abacaaba	aba	3

위와 같은 경우 접두사와 접미사가 일치하는 경우에 문자열 매칭을 탐색할 때 점프를 할 수 있어서 굉장히 효율적으로 작동하게 된다.

예시를 통해 알아보자.

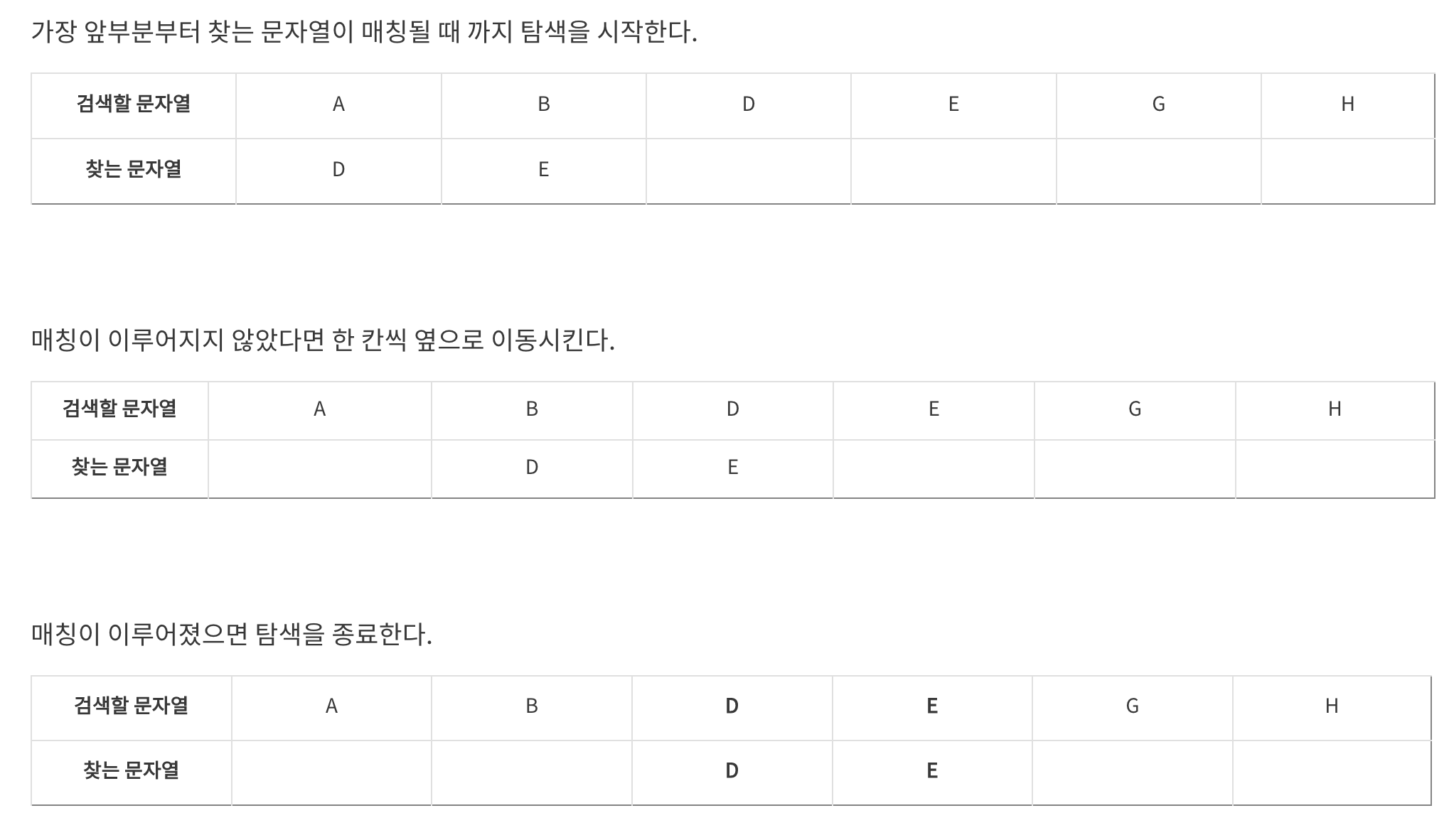
• 검색할 문자열(parent) : ababacabacaaba
• 찾는 문자열(find) : abacaaba

1. 찾는 문자열(find)의 접두사 접미사 최대길이 저장하는 table[] 배열을 생성한다.

 static int[] makeTable(String pattern) {
        int n = pattern.length();
        int[] table = new int[n];

        int idx=0;
        for(int i=1; i<n; i++) {
            while(idx>0 && pattern.charAt(i) != pattern.charAt(idx)) {
                idx = table[idx-1];
            }

            if(pattern.charAt(i) == pattern.charAt(idx)) {
                idx += 1;
                table[i] = idx;
            }
        }

        return table;
    }

이렇게 접두사와 접미사가 일치하는 최대길이를 찾았는데 이것으로 무엇을 어떻게 해야할까?

2. table[]을 가지고 점프하면서 문자열을 탐색한다.

  static void KMP(String parent, String pattern) {
        int[] table = makeTable(pattern);

        int n1 = parent.length();
        int n2 = pattern.length();

        int idx = 0; // 현재 대응되는 글자 수
        for(int i=0; i< n1; i++) {
            // idx번 글자와 짚더미의 해당 글자가 불일치할 경우,
            // 현재 대응된 글자의 수를 table[idx-1]번으로 줄인다.
            while(idx>0 && parent.charAt(i) != pattern.charAt(idx)) {
                idx = table[idx-1];
            }
            // 글자가 대응될 경우
            if(parent.charAt(i) == pattern.charAt(idx)) {
                if(idx == n2-1) {
                    //System.out.println(i-idx+1 + "번째에서 찾았습니다. ~" + (i+1) );
                    flag = true;
                    idx =table[idx];
                }else {
                    idx += 1;
                }
            }
        }
    }

• 만약 parent(i) == pattern(idx)가 같다면 즉, 접두사와 접미사가 같다면 슬라이딩 윈도우 처럼 이동하며 계속 비교한다.
  • 만약 parent(i) == pattern(idx)가 다르다면 즉, 접두사와 접미사가 다르다면 해당 칸 부터 다시 비교한다.
    • 단 table[]을 구해놨다. 비교 직전까지 값을 table과 비교하고 idx = table[idx-1] 해준다.

parent	a	b	c	d	a	b	c	d	a
pattern	a	b	c	d	a	b	d	d
비교	a==a(ok) idx++	b==b(ok) idx++	c==c(ok) idx++	d==d idx++	a==a idx++	b==b idx++	c!=d idx=table[idx-1]
i	0	1	2	3	4	5	6	7	8
idx	0	1	2	3	4	5	6	2

parent	a	b	c	d	a	b	c	d	a	b	d
pattern					a	b	c	d	a	b	d
비교	a==a(ok) idx++	b==b(ok) idx++	c==c(ok) idx++	d==d idx++	a==a idx++	b==b idx++	c!=d idx=table[idx-1]
i	0	1	2	3	4	5	6	7	8	9	10
idx					0	1	2	3